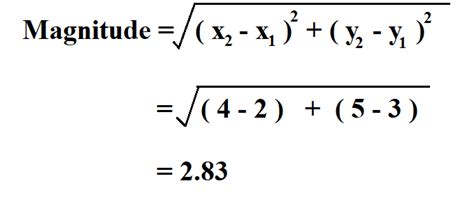How to Calculate Magnitude: A Comprehensive Guide
Understanding magnitude is crucial across various fields, from earthquake measurement to star brightness and even vector calculations in physics. This guide will break down how to calculate magnitude in different contexts, ensuring you grasp the core principles and relevant formulas.
Magnitude in Different Contexts
The term "magnitude" doesn't have a single definition. Its meaning depends heavily on the field of study. We'll explore some common applications:
1. Earthquake Magnitude: The Richter Scale
The Richter scale, while less commonly used now, provides a familiar example of magnitude calculation. It's a logarithmic scale, meaning an increase of one magnitude represents a tenfold increase in amplitude. The formula is:
M = log₁₀(A) + B
Where:
- M is the magnitude
- A is the amplitude of the seismic waves (usually measured in micrometers)
- B is a correction factor that accounts for the distance between the seismograph and the epicenter.
Important Note: Modern seismology relies more on the moment magnitude scale (Mw), which is more accurate for larger earthquakes and doesn't saturate at high magnitudes like the Richter scale. The calculation for Mw is significantly more complex and involves detailed analysis of seismic wave patterns.
2. Magnitude of a Vector
In physics and mathematics, vectors possess both magnitude (length) and direction. Calculating the magnitude of a vector involves the Pythagorean theorem (or its higher-dimensional extensions).
For a 2D vector (x, y):
Magnitude = √(x² + y²)
For a 3D vector (x, y, z):
Magnitude = √(x² + y² + z²)
This principle extends to higher dimensions by simply adding the squares of all components under the square root.
3. Stellar Magnitude: Apparent and Absolute Magnitude
Astronomy uses a magnitude scale to describe the brightness of stars and other celestial objects. There are two key types:
-
Apparent Magnitude (m): This is a measure of how bright a star appears from Earth. It's based on a logarithmic scale, with brighter objects having lower magnitudes. Calculations are complex and involve sophisticated instruments and calibrations.
-
Absolute Magnitude (M): This represents the intrinsic brightness of a star, as if viewed from a standard distance (usually 10 parsecs). Converting apparent magnitude to absolute magnitude requires knowing the star's distance. Again, the precise calculations are beyond the scope of a simple explanation and require specialized astronomical tools and data.
4. Magnitude in Other Fields
The concept of magnitude extends to other areas, such as:
- Magnitude of a complex number: Involving the square root of the sum of the squares of the real and imaginary parts.
- Magnitude of a sound wave: Related to its intensity or loudness, often expressed in decibels.
- Magnitude in signal processing: Representing the strength or amplitude of a signal.
Tips for Accurate Magnitude Calculation
Regardless of the context, accurate magnitude calculation relies on:
- Precise Data: Using reliable and accurate input values is paramount.
- Appropriate Formula: Choosing the correct formula based on the specific application is essential.
- Unit Consistency: Ensuring consistent units throughout the calculation prevents errors.
- Using Tools: For complex calculations (like moment magnitude or absolute stellar magnitude), specialized software and tools are often necessary.
This comprehensive guide provides a foundational understanding of magnitude calculation across various disciplines. Remember to always identify the specific context and use the appropriate formula and methods for accurate results.