How to Do Proportions: A Comprehensive Guide
Understanding proportions is a fundamental skill applicable across numerous fields, from cooking and construction to art and advanced mathematics. This guide provides a clear, step-by-step approach to mastering proportions, regardless of your current skill level.
What are Proportions?
Proportions are mathematical statements indicating that two ratios are equivalent. A ratio is a comparison of two quantities. For example, the ratio of apples to oranges in a basket containing 3 apples and 6 oranges is 3:6 (or 3/6, which simplifies to 1/2). A proportion shows that two ratios are equal; for instance, 3:6 = 1:2. This means that for every one apple, there are two oranges.
Key Concepts: Understanding Ratios and Equivalence
Before delving into solving proportions, it's crucial to grasp the core concepts:
- Ratio: A comparison of two quantities, often expressed as a fraction (e.g., 1/2, 3/4) or with a colon (e.g., 1:2, 3:4).
- Equivalent Ratios: Ratios that represent the same proportional relationship. For example, 1/2, 2/4, and 3/6 are all equivalent ratios.
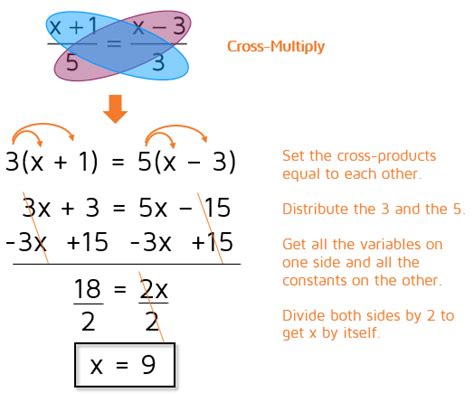
- Cross-Multiplication: A method used to solve proportions. It involves multiplying the numerator of one ratio by the denominator of the other and vice-versa. If the products are equal, the ratios are proportional.
Solving Proportions: Step-by-Step Guide
Let's tackle how to solve a proportion problem. Imagine you're baking a cake and the recipe calls for 2 cups of flour for every 3 cups of sugar. You want to make a larger cake and have 6 cups of sugar. How many cups of flour do you need?
1. Set up the Proportion:
First, set up the proportion, ensuring the units align. This is crucial to understanding the problem! We'll use 'x' to represent the unknown quantity (flour):
2 cups flour / 3 cups sugar = x cups flour / 6 cups sugar
2. Cross-Multiply:
Cross-multiply the terms:
2 * 6 = 3 * x
3. Simplify and Solve:
This simplifies to:
12 = 3x
Now, divide both sides by 3 to isolate 'x':
x = 12/3
x = 4
Therefore, you'll need 4 cups of flour.
Different Types of Proportion Problems
While the basic principle remains the same, proportion problems can appear in different forms:
- Direct Proportion: As one quantity increases, the other increases proportionally. (e.g., more hours worked, more money earned).
- Inverse Proportion: As one quantity increases, the other decreases proportionally. (e.g., more workers on a job, less time it takes to complete).
Solving both types uses the same core principles, but interpreting the relationship between the variables is key.
Real-World Applications of Proportions
Proportions are invaluable in everyday life:
- Cooking and Baking: Scaling recipes up or down.
- Construction and Engineering: Calculating dimensions and materials.
- Map Reading: Determining actual distances from map scales.
- Financial Calculations: Calculating interest rates, discounts, and percentages.
- Science: Converting units and analyzing experimental data.
Mastering Proportions: Practice Makes Perfect
The key to mastering proportions is practice. Work through numerous examples, starting with simple problems and gradually increasing complexity. Look for opportunities to apply your knowledge in everyday scenarios. The more you practice, the more intuitive solving proportions will become.