How to Find the Area of a Shape: A Comprehensive Guide
Finding the area of a shape is a fundamental concept in geometry with applications in various fields, from construction and design to land surveying and computer graphics. This guide will walk you through calculating the area of common shapes, providing formulas and practical examples. Mastering these techniques will significantly enhance your mathematical skills and problem-solving abilities.
Understanding Area
Before diving into specific shapes, let's clarify what "area" means. Area refers to the two-dimensional space occupied by a shape. It's measured in square units, such as square centimeters (cm²), square meters (m²), or square feet (ft²). The unit you use depends on the units used to measure the shape's dimensions.
Calculating the Area of Common Shapes
Here's a breakdown of how to calculate the area of several common geometric shapes:
1. Rectangle
A rectangle is a four-sided polygon with four right angles. To find its area, simply multiply its length (l) by its width (w).
Formula: Area = l * w
Example: A rectangle with a length of 5 cm and a width of 3 cm has an area of 5 cm * 3 cm = 15 cm².
2. Square
A square is a special type of rectangle where all four sides are equal in length. Therefore, its area is the side length (s) multiplied by itself.
Formula: Area = s²
Example: A square with a side length of 4 inches has an area of 4 inches * 4 inches = 16 square inches.
3. Triangle
The area of a triangle depends on its base (b) and height (h). The height is the perpendicular distance from the base to the opposite vertex.
Formula: Area = (1/2) * b * h
Example: A triangle with a base of 6 meters and a height of 4 meters has an area of (1/2) * 6 meters * 4 meters = 12 square meters.
4. Circle
The area of a circle is determined by its radius (r), which is the distance from the center to any point on the circle. The formula involves the mathematical constant π (pi), approximately equal to 3.14159.
Formula: Area = π * r²
Example: A circle with a radius of 2 cm has an area of π * (2 cm)² ≈ 12.57 cm².
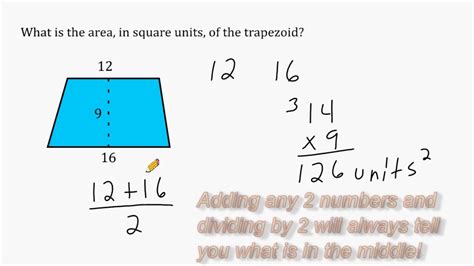
5. Trapezoid
A trapezoid is a quadrilateral with at least one pair of parallel sides. To find its area, you'll need the lengths of both parallel sides (a and b) and the height (h) between them.
Formula: Area = (1/2) * (a + b) * h
Example: A trapezoid with parallel sides of 5 feet and 7 feet, and a height of 3 feet, has an area of (1/2) * (5 feet + 7 feet) * 3 feet = 18 square feet.
Beyond the Basics: More Complex Shapes
Calculating the area of more complex shapes often involves breaking them down into simpler shapes (like rectangles, triangles, or circles) and summing the areas of the individual components. For irregular shapes, numerical methods such as integration might be necessary.
Practical Applications
Understanding how to calculate areas has numerous practical applications:
- Construction: Determining the amount of materials needed for flooring, painting, or roofing.
- Gardening: Planning garden layouts and calculating the amount of soil or fertilizer required.
- Real Estate: Calculating the size of land parcels or properties.
- Design: Creating and scaling designs in various fields like graphic design, architecture, or engineering.
By mastering the area formulas for basic shapes and understanding how to approach more complex figures, you'll equip yourself with a valuable skill applicable across many areas of life. Remember to always double-check your measurements and calculations to ensure accuracy.