Unlocking the Circle’s Secret: A Comprehensive Guide to Finding the Area of a Circle
Circles, those perfectly round shapes that seem to appear everywhere – from the wheels on our cars to the mesmerizing patterns in sunflowers – hold a certain mathematical allure. But beyond their aesthetic appeal, circles play a crucial role in various fields, from engineering and architecture to astronomy and computer graphics. Understanding their properties, particularly how to calculate their area, is fundamental. So, let’s embark on a journey to unravel the mystery behind finding the area of a circle!
Why is Knowing the Area of a Circle Important?
Before diving into the formula itself, it’s worth pondering why knowing how to calculate the area of a circle is so important. The applications are vast and varied:
- Construction and Architecture: Calculating the amount of material needed for circular structures like domes, circular windows, or even swimming pools.
- Engineering: Determining the cross-sectional area of pipes or cylindrical objects for fluid dynamics calculations.
- Manufacturing: Calculating the amount of material needed to produce circular products like gears, discs, or lenses.
- Agriculture: Estimating the area covered by circular irrigation systems.
- Everyday Life: Figuring out how much pizza you’re actually getting when ordering a pie based on its diameter, or determining the coverage of a circular rug in your living room.
These are just a few examples, but they highlight the practical significance of understanding how to find the area of a circle. It’s a skill that transcends the classroom and finds its way into real-world problem-solving.
The Key Players: Radius and Pi (π)
To calculate the area of a circle, we need to understand two key components: the radius and the mathematical constant Pi (π). Let’s break them down:
The Radius (r)
The radius of a circle is the distance from the center of the circle to any point on its edge. Imagine drawing a straight line from the very middle of the circle to its outer boundary – that line represents the radius. The radius is crucial because it’s the foundation upon which we build our area calculation.
Pi (π): The Circle’s Constant Companion
Pi (π) is a fascinating number. It’s an irrational number, meaning its decimal representation goes on forever without repeating. It represents the ratio of a circle’s circumference (the distance around the circle) to its diameter (the distance across the circle through the center). While its exact value is infinite, we often use approximations like 3.14 or 22/7 for practical calculations. Pi is a fundamental constant in mathematics and appears in various formulas beyond just the area of a circle.
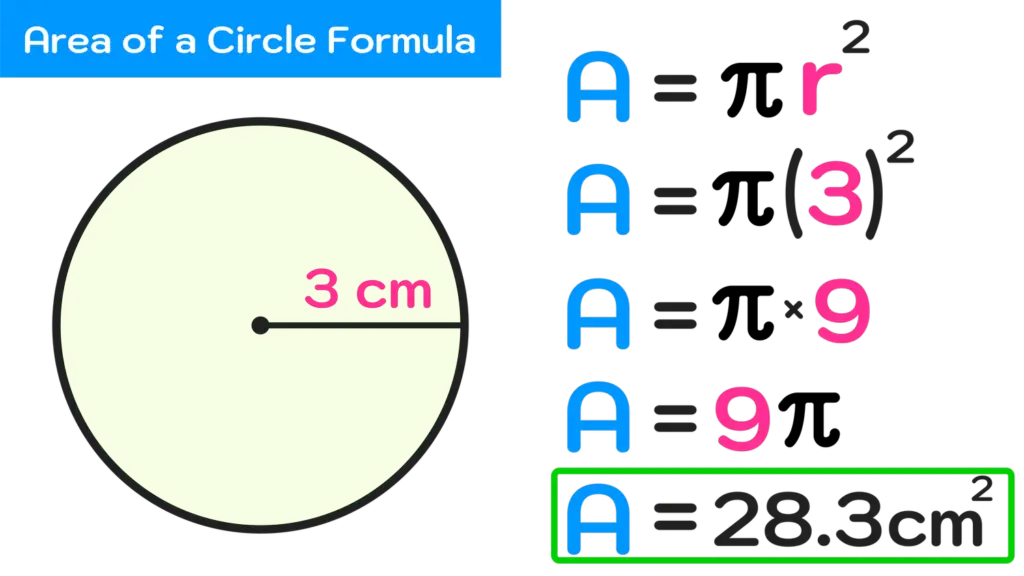
The Formula: A = πr²
Now for the moment we’ve all been waiting for: the formula for calculating the area of a circle! It’s elegantly simple:
A = πr²
Where:
- A represents the area of the circle.
- π represents Pi (approximately 3.14 or 22/7).
- r represents the radius of the circle.
- r² means the radius squared (radius multiplied by itself).
In essence, the formula tells us that the area of a circle is equal to Pi multiplied by the square of its radius. This formula is the key to unlocking the area of any circle, regardless of its size.
Putting the Formula into Action: Step-by-Step Examples
Let’s solidify our understanding with a few examples. We’ll walk through the process step-by-step, so you can see how the formula is applied in practice.
Example 1: Finding the Area with a Given Radius
Suppose we have a circle with a radius of 5 centimeters. Let’s calculate its area.
- Identify the radius: r = 5 cm
- Choose an approximation for Pi: Let’s use π = 3.14
- Apply the formula: A = πr² = 3.14 * (5 cm)² = 3.14 * 25 cm² = 78.5 cm²
Therefore, the area of the circle is approximately 78.5 square centimeters. Remember to include the units (square centimeters in this case) to indicate that we’re measuring area.
Example 2: Finding the Area with a Given Diameter
Sometimes, instead of the radius, we’re given the diameter of the circle. Remember that the diameter is twice the radius. So, to find the radius, we simply divide the diameter by 2.
Let’s say we have a circle with a diameter of 10 inches. Let’s calculate its area.
- Find the radius: r = diameter / 2 = 10 inches / 2 = 5 inches
- Choose an approximation for Pi: Let’s use π = 3.14
- Apply the formula: A = πr² = 3.14 * (5 inches)² = 3.14 * 25 inches² = 78.5 inches²
Therefore, the area of the circle is approximately 78.5 square inches.
Example 3: Using a Different Approximation for Pi
Let’s try using the approximation π = 22/7 in this example. Suppose we have a circle with a radius of 7 meters. Let’s calculate its area.
- Identify the radius: r = 7 m
- Choose an approximation for Pi: Let’s use π = 22/7
- Apply the formula: A = πr² = (22/7) * (7 m)² = (22/7) * 49 m² = 22 * 7 m² = 154 m²
Therefore, the area of the circle is 154 square meters. Notice that using 22/7 can sometimes simplify the calculation, especially when the radius is a multiple of 7.
Beyond the Basics: More Complex Scenarios
While the basic formula is straightforward, things can get a bit more interesting when dealing with more complex scenarios. Let’s explore a few:
Finding the Area of a Sector
A sector of a circle is a pie-shaped portion of the circle, bounded by two radii and the arc connecting them. To find the area of a sector, we need to know the central angle (θ) of the sector, measured in degrees.
The formula for the area of a sector is:
Area of Sector = (θ / 360°) * πr²
In other words, we’re finding the fraction of the entire circle that the sector represents and then multiplying that fraction by the area of the whole circle.
For example, if a sector has a central angle of 90° and a radius of 4 cm, its area would be:
Area of Sector = (90° / 360°) * π(4 cm)² = (1/4) * π * 16 cm² = 4π cm² ≈ 12.56 cm²
Finding the Area of an Annulus (Ring)
An annulus is the region between two concentric circles (circles with the same center but different radii). Imagine a donut shape – that’s an annulus.
To find the area of an annulus, we need to know the radii of both circles: the outer radius (R) and the inner radius (r).
The formula for the area of an annulus is:
Area of Annulus = πR² – πr² = π(R² – r²)
We’re simply finding the area of the larger circle and subtracting the area of the smaller circle.
For example, if the outer radius is 6 inches and the inner radius is 4 inches, the area of the annulus would be:
Area of Annulus = π(6² – 4²) = π(36 – 16) = π(20) ≈ 62.83 square inches.
Tips and Tricks for Accurate Calculations
Here are a few tips to ensure you’re calculating the area of a circle accurately:
- Pay Attention to Units: Always include the correct units in your answer (e.g., cm², m², inches²). Using the wrong units can lead to significant errors.
- Use the Correct Radius: Double-check that you’re using the radius and not the diameter in the formula. If you’re given the diameter, remember to divide it by 2 to find the radius.
- Choose an Appropriate Approximation for Pi: While 3.14 is a common approximation, using 22/7 can be more convenient when the radius is a multiple of 7. For even greater accuracy, use the Pi button on your calculator.
- Double-Check Your Work: It’s always a good idea to double-check your calculations to avoid simple errors.
- Use a Calculator: For complex calculations, especially when dealing with decimals, a calculator can help you avoid mistakes.
Common Mistakes to Avoid
Here are some common mistakes people make when calculating the area of a circle:
- Confusing Radius and Diameter: This is perhaps the most common mistake. Remember that the radius is half the diameter.
- Forgetting to Square the Radius: The formula requires you to square the radius (r²), not just multiply it by Pi.
- Using the Wrong Units: As mentioned earlier, using the wrong units can lead to significant errors. Make sure to use square units for area.
- Rounding Too Early: If you’re using an approximation for Pi, avoid rounding too early in the calculation. Rounding too early can introduce errors in your final answer.
The Circle’s Enduring Significance
The circle, with its elegant symmetry and fundamental properties, continues to fascinate mathematicians, scientists, and artists alike. Understanding how to calculate its area is not just a mathematical exercise; it’s a gateway to understanding the world around us. From the smallest gears to the largest celestial bodies, circles play a vital role, and knowing how to find their area is a valuable skill that will serve you well in various aspects of life.
Real-World Applications of Circle Area Calculation
To further illustrate the importance of understanding how to calculate the area of a circle, let’s delve into some specific real-world applications:
- Landscaping: When designing a circular flower bed or a round patio, calculating the area is crucial for determining the amount of materials needed, such as soil, mulch, paving stones, or concrete.
- Cooking and Baking: When making a pizza or a pie, knowing the area helps determine the amount of dough, sauce, and toppings required to fill the circular pan.
- HVAC (Heating, Ventilation, and Air Conditioning): Calculating the cross-sectional area of circular ducts is essential for determining airflow and ensuring efficient heating and cooling systems.
- Optics: The area of a lens determines the amount of light it can gather, which is crucial in designing telescopes, microscopes, and cameras.
- Fluid Mechanics: Calculating the cross-sectional area of pipes and tubes is essential for determining the flow rate of liquids and gases in various engineering applications.
These examples demonstrate that the ability to calculate the area of a circle is not just a theoretical concept but a practical skill that has numerous real-world applications across various industries and fields.
Advanced Concepts Related to Circle Area
For those who want to delve deeper into the mathematics of circles, here are some advanced concepts related to circle area:
- Integration: The area of a circle can be derived using integral calculus, which provides a more rigorous and fundamental understanding of the concept.
- Polar Coordinates: Circles are often represented using polar coordinates, which simplify calculations involving angles and distances from the center.
- Geometric Transformations: Understanding how geometric transformations, such as scaling and rotation, affect the area of a circle is crucial in various applications, such as computer graphics and image processing.
- Isoperimetric Inequality: This inequality states that among all closed curves of the same length, the circle encloses the largest area. This principle has important implications in optimization problems.
Conclusion: Mastering the Circle’s Area
In conclusion, understanding how to find the area of a circle is a fundamental skill with wide-ranging applications. By mastering the formula A = πr² and practicing with various examples, you can confidently tackle problems involving circular shapes in various contexts. From everyday tasks to complex engineering projects, the ability to calculate the area of a circle will prove to be a valuable asset. So, embrace the circle, unlock its secrets, and appreciate its enduring significance in the world around us. Now you’re equipped to tackle any circle-related area problem that comes your way!

