Home » Fractions » Mastering Fraction Division: A Comprehensive Guide with Multiplication Techniques
Posted in

Mastering Fraction Division: A Comprehensive Guide with Multiplication Techniques

Caroline Secondaby Caroline Seconda••Posted inFractions, Mathematics•, , , , ,

Mastering Fraction Division

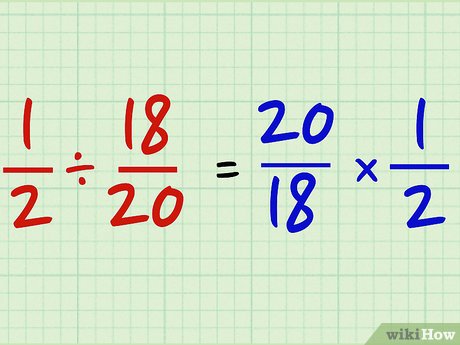
Mastering Fraction Division: A Comprehensive Guide with Multiplication Techniques

Fractions, those seemingly simple yet sometimes perplexing numbers, are a fundamental part of mathematics. From everyday tasks like splitting a pizza to complex calculations in engineering, understanding fractions is crucial. While adding, subtracting, and multiplying fractions might seem straightforward, dividing them can often feel like a stumbling block. But fear not! This comprehensive guide will demystify the process of dividing fractions, revealing how it’s intimately linked to multiplication. We’ll explore the underlying concepts, provide step-by-step instructions, and offer plenty of examples to help you master this essential skill.

Understanding the Basics of Fractions

Before diving into division, let’s quickly review the basic components of a fraction. A fraction represents a part of a whole and consists of two numbers: the numerator and the denominator.

  • Numerator: The top number of the fraction, indicating how many parts of the whole you have.
  • Denominator: The bottom number of the fraction, indicating the total number of equal parts the whole is divided into.

For example, in the fraction 3/4, 3 is the numerator and 4 is the denominator. This means you have 3 parts out of a total of 4 equal parts.

It’s also important to understand the concept of reciprocals. The reciprocal of a number is simply 1 divided by that number. For a fraction, the reciprocal is found by swapping the numerator and the denominator. For instance, the reciprocal of 2/5 is 5/2. Understanding reciprocals is key to understanding fraction division.

The Core Concept: Dividing by a Fraction is Multiplying by its Reciprocal

The golden rule of dividing fractions is this: Dividing by a fraction is the same as multiplying by its reciprocal. This seemingly simple statement unlocks the secret to fraction division. Instead of trying to figure out how many times one fraction fits into another (which can be conceptually challenging), you transform the division problem into a multiplication problem, which is often easier to handle.

Why does this work? Think of division as the inverse operation of multiplication. When you divide by a number, you’re essentially asking, “What number, when multiplied by this divisor, gives me the dividend?” Using the reciprocal allows us to reframe the question in terms of multiplication.

Let’s illustrate this with a simple example: 6 ÷ 1/2. This is asking, “How many halves are there in 6?” Intuitively, we know the answer is 12. Now, let’s apply the rule: 6 ÷ 1/2 = 6 × 2/1 = 6 × 2 = 12. See? It works!

Step-by-Step Guide to Dividing Fractions

Now that we understand the underlying principle, let’s break down the process of dividing fractions into a series of easy-to-follow steps:

  1. Identify the dividend and the divisor: The dividend is the number being divided, and the divisor is the number you’re dividing by. For example, in the problem 3/4 ÷ 1/2, 3/4 is the dividend and 1/2 is the divisor.
  2. Find the reciprocal of the divisor: Flip the divisor fraction by swapping the numerator and the denominator. In our example, the reciprocal of 1/2 is 2/1.
  3. Change the division sign to a multiplication sign: Replace the division symbol (÷) with a multiplication symbol (×). So, 3/4 ÷ 1/2 becomes 3/4 × 2/1.
  4. Multiply the numerators: Multiply the numerators of the two fractions. In our example, 3 × 2 = 6.
  5. Multiply the denominators: Multiply the denominators of the two fractions. In our example, 4 × 1 = 4.
  6. Simplify the resulting fraction: If possible, simplify the fraction to its lowest terms. In our example, 6/4 can be simplified to 3/2. This can also be expressed as the mixed number 1 1/2.

Examples of Dividing Fractions

Let’s work through some more examples to solidify your understanding:

Example 1: Dividing a Fraction by a Fraction

Problem: 2/3 ÷ 4/5

  1. Dividend: 2/3, Divisor: 4/5
  2. Reciprocal of 4/5: 5/4
  3. 2/3 ÷ 4/5 = 2/3 × 5/4
  4. Multiply numerators: 2 × 5 = 10
  5. Multiply denominators: 3 × 4 = 12
  6. Result: 10/12
  7. Simplify: 10/12 = 5/6

Therefore, 2/3 ÷ 4/5 = 5/6

Example 2: Dividing a Whole Number by a Fraction

Problem: 5 ÷ 1/3

Remember that any whole number can be written as a fraction with a denominator of 1. So, 5 can be written as 5/1.

  1. Dividend: 5/1, Divisor: 1/3
  2. Reciprocal of 1/3: 3/1
  3. 5/1 ÷ 1/3 = 5/1 × 3/1
  4. Multiply numerators: 5 × 3 = 15
  5. Multiply denominators: 1 × 1 = 1
  6. Result: 15/1
  7. Simplify: 15/1 = 15

Therefore, 5 ÷ 1/3 = 15

Example 3: Dividing a Fraction by a Whole Number

Problem: 3/8 ÷ 2

Again, write the whole number as a fraction with a denominator of 1. So, 2 becomes 2/1.

  1. Dividend: 3/8, Divisor: 2/1
  2. Reciprocal of 2/1: 1/2
  3. 3/8 ÷ 2/1 = 3/8 × 1/2
  4. Multiply numerators: 3 × 1 = 3
  5. Multiply denominators: 8 × 2 = 16
  6. Result: 3/16

Therefore, 3/8 ÷ 2 = 3/16

Example 4: Dividing Mixed Numbers

Problem: 2 1/2 ÷ 1 1/4

Before you can divide mixed numbers, you need to convert them into improper fractions.

  • Convert 2 1/2 to an improper fraction: (2 × 2) + 1 = 5, so 2 1/2 = 5/2
  • Convert 1 1/4 to an improper fraction: (1 × 4) + 1 = 5, so 1 1/4 = 5/4

Now we have the problem: 5/2 ÷ 5/4

  1. Dividend: 5/2, Divisor: 5/4
  2. Reciprocal of 5/4: 4/5
  3. 5/2 ÷ 5/4 = 5/2 × 4/5
  4. Multiply numerators: 5 × 4 = 20
  5. Multiply denominators: 2 × 5 = 10
  6. Result: 20/10
  7. Simplify: 20/10 = 2

Therefore, 2 1/2 ÷ 1 1/4 = 2

Tips and Tricks for Dividing Fractions

  • Always simplify your answer: After multiplying and obtaining the result, always check if the fraction can be simplified to its lowest terms. This makes the answer cleaner and easier to understand.
  • Convert mixed numbers to improper fractions first: When dealing with mixed numbers, always convert them into improper fractions before performing any division. This avoids confusion and ensures accurate results.
  • Remember the reciprocal: The most common mistake is forgetting to flip the divisor fraction. Double-check that you’ve found the reciprocal correctly before proceeding with the multiplication.
  • Practice makes perfect: The more you practice dividing fractions, the more comfortable and confident you’ll become. Work through various examples and try different types of problems.
  • Use visual aids: If you’re struggling to grasp the concept, try using visual aids like fraction bars or pie charts. These can help you visualize the division process and understand what’s happening with the fractions.

Common Mistakes to Avoid

While the process of dividing fractions is relatively straightforward, there are a few common mistakes that students often make. Being aware of these pitfalls can help you avoid them.

  • Forgetting to flip the divisor: This is the most common mistake. Remember that you need to multiply by the reciprocal of the divisor, not the divisor itself.
  • Flipping the dividend instead of the divisor: Make sure you’re flipping the fraction you’re dividing by, not the fraction you’re dividing into.
  • Not simplifying the answer: While not technically incorrect, leaving the answer in an unsimplified form is considered poor practice. Always reduce the fraction to its lowest terms.
  • Incorrectly converting mixed numbers: Double-check your calculations when converting mixed numbers to improper fractions. A small error here can lead to a completely wrong answer.
  • Confusing division with multiplication: While dividing fractions involves multiplication, it’s important to remember that the initial operation is division. Don’t skip the step of finding the reciprocal.

Real-World Applications of Dividing Fractions

Dividing fractions isn’t just an abstract mathematical concept; it has numerous practical applications in everyday life.

  • Cooking and Baking: Recipes often involve fractions. If you need to halve or double a recipe, you’ll need to divide or multiply fractions to adjust the ingredient amounts.
  • Construction and Carpentry: Measuring lengths and cutting materials often involves fractions. Dividing fractions is essential for calculating proportions and ensuring accurate cuts.
  • Sewing and Quilting: Similar to construction, sewing and quilting require precise measurements. Dividing fractions is used to determine fabric sizes and create accurate patterns.
  • Sharing and Dividing Resources: Dividing a pizza, splitting a bill, or sharing a bag of candy all involve dividing fractions to ensure fair distribution.
  • Calculating Time and Distance: If you know the total distance of a trip and the fraction of the trip you’ve already completed, you can use division to calculate the remaining distance.

Advanced Topics in Fraction Division

Once you’ve mastered the basics of dividing fractions, you can explore more advanced topics:

  • Complex Fractions: These are fractions where the numerator, the denominator, or both contain fractions themselves. To simplify complex fractions, you often need to divide fractions within fractions.
  • Dividing Algebraic Fractions: In algebra, fractions can contain variables. Dividing algebraic fractions follows the same principles as dividing numerical fractions, but you need to apply algebraic rules to simplify the expressions.
  • Applications in Calculus: Fractions and their derivatives play a crucial role in calculus. Understanding fraction division is essential for solving problems involving rates of change and optimization.

Conclusion

Dividing fractions might have seemed daunting at first, but with a clear understanding of the underlying concepts and a step-by-step approach, it becomes a manageable and even enjoyable task. Remember the golden rule: dividing by a fraction is the same as multiplying by its reciprocal. Practice regularly, avoid common mistakes, and explore real-world applications to solidify your knowledge. With dedication and persistence, you’ll master fraction division and unlock a valuable skill that will serve you well in mathematics and beyond. So, embrace the challenge, dive into the world of fractions, and discover the power of division!

Hi, I'm Caroline, the writer behind this how-to blog! I love sharing practical tips and simple solutions for everyday life. I turn complex ideas into easy-to-follow guides. My goal is to help you tackle challenges with clear, inspiring advice. When not writing, I enjoy cooking and learning. Follow along for useful tips and fresh ideas!

Leave a Reply

Your email address will not be published. Required fields are marked *