How to Find the Standard Error: A Comprehensive Guide
Understanding standard error is crucial for interpreting statistical data and drawing meaningful conclusions. It's a measure of the statistical accuracy of an estimate, essentially telling us how much our sample mean is likely to vary from the true population mean. This guide will walk you through calculating standard error, explaining its importance and offering practical examples.
What is Standard Error?
The standard error (SE) quantifies the variability of a sample statistic (like the mean) across multiple samples drawn from the same population. A smaller standard error indicates a more precise estimate of the population parameter. Conversely, a larger standard error suggests more variability and less confidence in the sample's representation of the population. It's not the same as the standard deviation, which measures the spread of individual data points within a single sample.
How to Calculate Standard Error
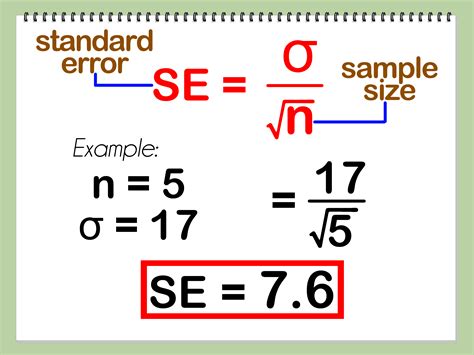
The formula for calculating the standard error of the mean is:
SE = Standard Deviation / √(Sample Size)
Where:
- Standard Deviation (SD): A measure of the dispersion or spread of the data points in your sample. You can calculate this using various methods, typically involving finding the average squared difference from the mean. Many statistical software packages and calculators can do this automatically.
- √(Sample Size): The square root of the number of observations (data points) in your sample.
Step-by-Step Calculation:
Let's illustrate with an example. Suppose you have a sample of 25 students' test scores with a mean of 75 and a standard deviation of 10.
- Identify the standard deviation (SD): SD = 10
- Determine the sample size (n): n = 25
- Calculate the square root of the sample size: √25 = 5
- Apply the formula: SE = 10 / 5 = 2
Therefore, the standard error of the mean for this example is 2. This means that the sample mean of 75 has a standard error of 2, indicating a certain level of uncertainty around the true population mean.
Understanding the Implications of Standard Error
A smaller standard error implies a more precise estimate. This higher precision stems from either a larger sample size (reducing the impact of random sampling error) or a smaller standard deviation (indicating less variability within the sample itself).
Factors Affecting Standard Error:
- Sample Size: Larger samples generally lead to smaller standard errors. This is because larger samples provide a more accurate representation of the population.
- Standard Deviation: A smaller standard deviation within the sample leads to a smaller standard error. This indicates less variability in the data.
Standard Error vs. Standard Deviation: Key Differences
It's vital to distinguish between standard error and standard deviation:
- Standard Deviation: Measures the spread or dispersion of individual data points within a single sample.
- Standard Error: Measures the variability of the sample statistic (e.g., the mean) across multiple samples from the same population.
Conclusion
Calculating and interpreting standard error is essential for understanding the reliability and precision of statistical inferences. By understanding the factors influencing standard error and its relationship to standard deviation, you can better analyze data and draw more confident conclusions. Remember to use appropriate statistical software or calculators to simplify the calculations, especially for larger datasets.