How to Get Wavelength from Frequency: A Simple Guide
Understanding the relationship between wavelength and frequency is fundamental in physics and many related fields. This guide will show you how to easily calculate wavelength from frequency, providing you with the necessary formulas and examples. We'll also explore the practical applications of this knowledge.
Understanding the Basics: Wavelength and Frequency
Before diving into the calculations, let's define our key terms:
-
Wavelength (λ): This represents the distance between two consecutive crests (or troughs) of a wave. It's typically measured in meters (m), centimeters (cm), or nanometers (nm).
-
Frequency (f): This indicates the number of wave cycles that pass a fixed point per unit of time. It's usually measured in Hertz (Hz), which is equivalent to cycles per second (cps).
-
Speed (v): This refers to the speed at which the wave travels through a medium. For electromagnetic waves (like light), the speed is the speed of light (c), approximately 3 x 10<sup>8</sup> m/s in a vacuum. For other types of waves, the speed will depend on the medium.
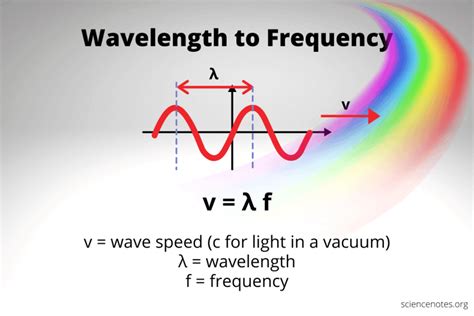
The Fundamental Formula: Connecting Wavelength and Frequency
The core relationship between wavelength (λ), frequency (f), and speed (v) is given by the following equation:
v = fλ
This means: Speed = Frequency x Wavelength
To find the wavelength (λ) when you know the frequency (f) and the speed (v), simply rearrange the formula:
λ = v / f
Calculating Wavelength: Step-by-Step Examples
Let's work through some examples to solidify your understanding:
Example 1: Electromagnetic Wave
Problem: A radio wave has a frequency of 100 MHz (100 x 10<sup>6</sup> Hz). What is its wavelength?
Solution:
-
Identify the known values: f = 100 x 10<sup>6</sup> Hz; v = c = 3 x 10<sup>8</sup> m/s (speed of light).
-
Use the formula: λ = v / f
-
Substitute the values: λ = (3 x 10<sup>8</sup> m/s) / (100 x 10<sup>6</sup> Hz)
-
Calculate: λ = 3 meters
Therefore, the wavelength of the radio wave is 3 meters.
Example 2: Sound Wave
Problem: A sound wave has a frequency of 440 Hz and travels at a speed of 343 m/s in air. What is its wavelength?
Solution:
-
Identify the known values: f = 440 Hz; v = 343 m/s
-
Use the formula: λ = v / f
-
Substitute the values: λ = (343 m/s) / (440 Hz)
-
Calculate: λ ≈ 0.78 meters
Therefore, the wavelength of the sound wave is approximately 0.78 meters.
Practical Applications
Understanding the relationship between wavelength and frequency has wide-ranging applications across various scientific and engineering disciplines, including:
-
Electromagnetic Spectrum: Analyzing radio waves, microwaves, infrared radiation, visible light, ultraviolet radiation, X-rays, and gamma rays.
-
Acoustics: Studying sound waves and their properties.
-
Oceanography: Investigating ocean waves and their behavior.
-
Seismology: Understanding seismic waves and earthquake activity.
-
Medical Imaging: Utilizing techniques like ultrasound and MRI that rely on wave properties.
Conclusion
Calculating wavelength from frequency is straightforward using the simple formula λ = v / f. By understanding this fundamental relationship and applying the appropriate speed of the wave, you can easily determine the wavelength for various wave types. This knowledge is crucial for various applications across many scientific and engineering fields. Remember to always use consistent units for accurate calculations.